Embedded atom model

In computational chemistry and computational physics, the embedded atom model, embedded-atom method or EAM, is an approximation describing the energy between atoms, an interatomic potential. The energy is a function of a sum of functions of the separation between an atom and its neighbors. In the original model, by Murray Daw and Mike Baskes, the latter functions represent the electron density. EAM is related to the second moment approximation to tight binding theory, also known as the Finnis-Sinclair model. These models are particularly appropriate for metallic systems. Embedded-atom methods are widely used in molecular dynamics simulations.

Model simulation

In a simulation, the potential energy of an atom, 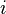i\!, is given by[1]

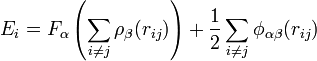E_i = F_\alpha\left(\sum_{i\neq j} \rho_\beta (r_{ij}) \right) + \frac{1}{2} \sum_{i\neq j} \phi_{\alpha\beta}(r_{ij}),

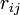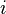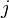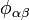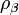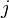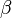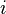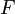where r_{ij}\! is the distance between atoms i\! and j\!, \phi_{\alpha\beta} is a pair-wise potential function, \rho_\beta\! is the contribution to the electron charge density from atom j\! of type \beta\! at the location of atom i\!, and F\! is an embedding function that represents the energy required to place atom 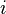i\! of type 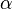\alpha\! into the electron cloud.

Since the electron cloud density is a summation over many atoms, usually limited by a cutoff radius, the EAM potential is a multibody potential. For a single element system of atoms, three scalar functions must be specified: the embedding function, a pair-wise interaction, and an electron cloud contribution function. For a binary alloy, the EAM potential requires seven functions: three pair-wise interactions (A-A, A-B, B-B), two embedding functions, and two electron cloud contribution functions. Generally these functions are provided in a tabularized format and interpolated by cubic splines.

See also

References

  1. ↑ "Pair - EAM". LAMMPS Molecular Dynamics Simulator. Retrieved 2008-10-01.
This article is issued from Wikipedia - version of the 12/26/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.