Edmonds–Karp algorithm

In computer science, the Edmonds–Karp algorithm is an implementation of the Ford–Fulkerson method for computing the maximum flow in a flow network in O(V E²) time. The algorithm was first published by Yefim Dinitz in 1970^[1][2] and independently published by Jack Edmonds and Richard Karp in 1972.^[3] Dinic's algorithm includes additional techniques that reduce the running time to O(V²E).

Algorithm

The algorithm is identical to the Ford–Fulkerson algorithm, except that the search order when finding the augmenting path is defined. The path found must be a shortest path that has available capacity. This can be found by a breadth-first search, as we let edges have unit length. The running time of O(V E²) is found by showing that each augmenting path can be found in O(E) time, that every time at least one of the E edges becomes saturated (an edge which has the maximum possible flow), that the distance from the saturated edge to the source along the augmenting path must be longer than last time it was saturated, and that the length is at most V. Another property of this algorithm is that the length of the shortest augmenting path increases monotonically. There is an accessible proof in Introduction to Algorithms.^[4]

Pseudocode

The Wikibook Algorithm implementation has a page on the topic of: Edmonds-Karp

For a more high level description, see Ford–Fulkerson algorithm.

algorithm EdmondsKarp
    input:
        C[1..n, 1..n] (Capacity matrix)
        T[1..n, 1..n] (Residual matrix) T is equal to C initially
        s             (Source)
        t             (Sink)
    output:
        f             (Value of maximum flow)
        F             (A matrix giving a legal flow with the maximum value)
    f := 0 (Initial flow is zero)
    F := array(1..n, 1..n) (Flow matrix)
    forever
        m, P := BreadthFirstSearch(C, T, s, t, F)
        if m = 0
            break
        f := f + m
        (Backtrack search, and write flow)
        v := t
        while v ≠ s
            u := P[v]
            F[u,v] := F[u,v] + m
            F[v,u] := F[v,u] - m
            T[u,v] := T[u,v] - m
            T[v,u] := T[v,u] + m
            v := u
    return (f, F)

algorithm BreadthFirstSearch
    input:
        C, T, s, t, F
    output:
        M[t]          (Capacity of path found)
        P             (Parent table)
    P := array(1..n)
    for u in 1..n
        P[u] := -1
    P[s] := -2 (make sure source is not rediscovered)
    M := array(1..n) (Capacity of found path to node)
    M[s] := ∞
    Q := queue()
    Q.offer(s)
    while Q.size() > 0
        u := Q.poll()
        for each node in graph except u
            (If there is available residual capacity, and v is not seen before in search)
            if T[u,v] > 0 and P[v] = -1
                P[v] := u
                M[v] := min(M[u], C[u,v] - F[u,v])
                if v ≠ t
                    Q.offer(v)
                else
                    return M[t], P
    return 0, P

EdmondsKarp pseudo code using Adjacency nodes.

algorithm EdmondsKarp
    input:
        graph   (graph[v] should be the list of edges coming out of vertex v.
                 Each edge should have a capacity, flow, source and sink as parameters,
                 as well as a pointer to the reverse edge.)
        s       (Source vertex)
        t       (Sink vertex)
    output:
        flow    (Value of maximum flow)
    
    flow := 0   (Initial flow to zero)
    repeat
        (Run a bfs to find the shortest s-t path.
         We use 'pred' to store the edge taken to get to each vertex,
         so we can recover the path afterwards)
        q := queue()
        q.push(s)
        pred := array(graph.length)
        while not empty(q)
            cur := q.poll()
            for Edge e in graph[cur]
                 if pred[e.t] = null and e.t ≠ s and e.cap > e.flow
                    pred[e.t] := e
                    q.push(e.t)
        
        (Stop if we weren't able to find a path from s to t)
        if pred[t] = null
            break
        
        (Otherwise see how much flow we can send)
        df := ∞
        for (e := pred[t]; e ≠ null; e := pred[e.s])
            df := min(df, e.cap - e.flow)
        
        (And update edges by that amount)
        for (e := pred[t]; e ≠ null; e := pred[e.s])
            e.flow  := e.flow + df
            e.rev.flow := e.rev.flow - df
        
        flow := flow + df
    return flow

Example

Given a network of seven nodes, source A, sink G, and capacities as shown below:

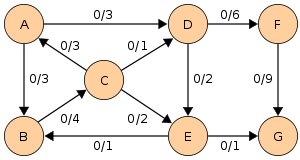
In the pairs written on the edges, is the current flow, and is the capacity. The residual capacity from to is , the total capacity, minus the flow that is already used. If the net flow from to is negative, it contributes to the residual capacity.

Capacity	Path	Resulting network

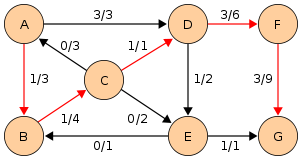Notice how the length of the augmenting path found by the algorithm (in red) never decreases. The paths found are the shortest possible. The flow found is equal to the capacity across the minimum cut in the graph separating the source and the sink. There is only one minimal cut in this graph, partitioning the nodes into the sets and , with the capacity

Notes

References

1. Algorithms and Complexity (see pages 63–69). http://www.cis.upenn.edu/~wilf/AlgComp3.html