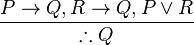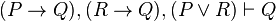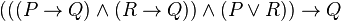Disjunction elimination
| Transformation rules |
|---|
| Propositional calculus |
| Rules of inference |
| Rules of replacement |
| Predicate logic |
In propositional logic, disjunction elimination[1][2] (sometimes named proof by cases, case analysis, or or elimination), is the valid argument form and rule of inference that allows one to eliminate a disjunctive statement from a logical proof. It is the inference that if a statement 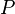 implies a statement
implies a statement 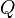 and a statement
and a statement 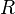 also implies
also implies 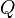 , then if either
, then if either 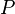 or
or 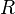 is true, then
is true, then 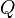 has to be true. The reasoning is simple: since at least one of the statements P and R is true, and since either of them would be sufficient to entail Q, Q is certainly true.
has to be true. The reasoning is simple: since at least one of the statements P and R is true, and since either of them would be sufficient to entail Q, Q is certainly true.
- If I'm inside, I have my wallet on me.
- If I'm outside, I have my wallet on me.
- It is true that either I'm inside or I'm outside.
- Therefore, I have my wallet on me.
It is the rule can be stated as:
where the rule is that whenever instances of "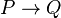 ", and "
", and "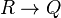 " and "
" and "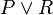 " appear on lines of a proof, "
" appear on lines of a proof, "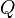 " can be placed on a subsequent line.
" can be placed on a subsequent line.
Formal notation
The disjunction elimination rule may be written in sequent notation:
where 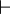 is a metalogical symbol meaning that
is a metalogical symbol meaning that 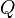 is a syntactic consequence of
is a syntactic consequence of 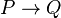 , and
, and 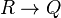 and
and 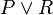 in some logical system;
in some logical system;
and expressed as a truth-functional tautology or theorem of propositional logic:
where 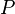 ,
, 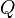 , and
, and 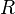 are propositions expressed in some formal system.
are propositions expressed in some formal system.