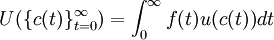Discount function
A discount function is used in economic models to describe the weights placed on rewards received at different points in time. For example, if time is discrete and utility is time-separable, with the discount function
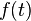 and with
and with 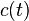 defined as consumption at time t,
defined as consumption at time t,
total utility is given by
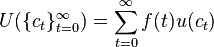 .
.
Total utility in the continuous-time case is given by
provided that this integral exists.
Exponential discounting and hyperbolic discounting are the two most commonly used examples.
See also
References
For a comprehensive review, see: Shane Frederick & George Loewenstein & Ted O'Donoghue, 2002. "Time Discounting and Time Preference: A Critical Review," Journal of Economic Literature, vol. 40(2), pages 351-401, June.
This article is issued from Wikipedia - version of the 1/1/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.