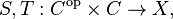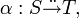Dinatural transformation

In category theory, a dinatural transformation 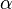$\alpha$ between two functors

S,T : C^{\mathrm{op}}\times C\to X,

written

\alpha : S\ddot\to T,

is a function which to every object c of C associates an arrow

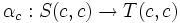\alpha_c : S(c,c)\to T(c,c)

of X

and satisfies the following coherence property: for every morphism 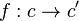$f:c\to c'$ of C the diagram

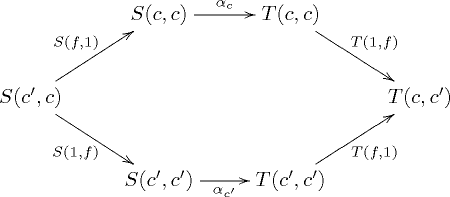
commutes.

The composition of two dinatural transformations need not be dinatural.

External links

This article is issued from Wikipedia - version of the 12/9/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.