Differential stress

Differential stress is the difference between the greatest and the least compressive stress experienced by an object. For both the geological and civil engineering convention 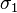$\sigma_1$ is the greatest compressive stress and 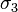$\sigma_3$ is the weakest,

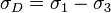$\!\sigma_D = \sigma_1 - \sigma_3$ .

In other engineering fields and in physics, 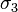$\sigma_3$ is the greatest compressive stress and 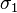$\sigma_1$ is the weakest, so

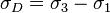$\!\sigma_D = \sigma_3 - \sigma_1$ .

These conventions originated because geologists and civil engineers (especially soil mechanicians) are often concerned with failure in compression, while many other engineers are concerned with failure in tension. A further reason for the second convention is that it allows a positive stress to cause a compressible object to increase in size, making the sign convention self-consistent.

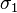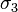In structural geology, differential stress is used to assess whether tensile or shear failure will occur when a Mohr circle (plotted using $\sigma_1$ and $\sigma_3$ ) touches the failure envelope of the rocks. If the differential stress is less than four times the tensile strength of the rock, then extensional failure will occur. If the differential stress is more than four times the tensile strength of the rock, then shear failure will occur.^[1]

References

↑ Cosgrove. J. W. (1998) The role of structural geology in reservoir characterization. Geological Society, London, Special Publications, v. 127; p. 1-13

This article is issued from Wikipedia - version of the 6/8/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.