Genus (music)
Genus (Gr.: γένος [genos], pl. γένη [genē], lat. genus, pl. genera "type, kind") is a term used in the Ancient Greek and Roman theory of music to describe certain classes of intonations of the two movable notes within a tetrachord.
Aristoxenus (in his fragmentary treatise on rhythm) names 'genera' some patterns of rhythm. The tetrachordal concept is also found in the modal theory of Byzantine music and relates to the jins of Arabic music.
Tetrachords
According to the system of Aristoxenus and his followers—Cleonides, Bacchius, Gaudentius, Alypius, Bryennius, and Aristides Quintilianus (Solomon 1980, vi)—the paradigmatic tetrachord was bounded by the fixed tones hypate and mese, which are a perfect fourth apart and do not vary from one genus to another. Between these are two movable notes, called parhypate and lichanos. The upper tone, lichanos, can vary over the range of a whole tone, whereas the lower note, parhypate, is restricted to the span of a quarter tone. However, their variation in position must always be proportional. This interval between the fixed hypate and movable parhypate cannot ever be larger than the interval between the two movable tones (Mathiesen 1999, 311–12, 326). When the composite of the two smaller intervals is less than the remaining (incomposite) interval, the three-note group is called pyknon (meaning "compressed"). The positioning of these two notes defined three genera: the diatonic, chromatic (also called chroma, "colour"), and enharmonic (also called ἁρμονία [harmonia]). The first two of these were subject to further variation, called shades—χρόαι (chroai)—or species—εἶδη (eidē). For Aristoxenus himself, these shades were dynamic: that is, they were not fixed in an ordered scale, and the shades were flexible along a continuum within certain limits. Instead, they described characteristic functional progressions of intervals, which he called "roads" (ὁδοί), possessing different ascending and descending patterns while nevertheless remaining recognisable. For his successors, however, the genera became fixed intervallic successions, and their shades became precisely defined subcategories (Mathiesen 2001a; Mathiesen 2001b). Furthermore, in sharp contrast to the Pythagoreans, Aristoxenos deliberately avoids numerical ratios. Instead, he defines a whole tone as the difference between a perfect fifth and a perfect fourth, and then divides that tone into semitones, third-tones, and quarter tones, to correspond to the diatonic, chromatic, and enharmonic genera, respectively (Mathiesen 1999, 310–11).
Diatonic
Aristoxenus describes the diatonic genus (Greek: διατονικό γένος) as the oldest and most natural of the genera (Mathiesen & 1999 310). It is the division of the tetrachord from which the modern diatonic scale evolved. The distinguishing characteristic of the diatonic genus is that its largest interval is about the size of a major second. The other two intervals vary according to the tunings of the various shades.
The word is derived either from the Greek, dia (διά) and tonos (τόνος), meaning "proceeding by whole tones" (Drabkin 1980), or "through, at the interval of" a "tone" (OED), or from Greek dia and tonikos, meaning "at intervals of a tone" (Dunsby 2002).
Shades
Aristoxenus (and Cleonides, following his example) describes two shades of the diatonic, which he calls "soft" and "syntonic" (Solomon 1980, 259).
Tunings
The traditional Pythagorean tuning of the diatonic, also known as Ptolemy's "ditonic diatonic", has two identical 9/8 tones in succession, making the other interval 256/243:
hypate parhypate lichanos mese | 256/243 | 9/8 | 9/8 | -498 -408 -204 0 centsPlay
However, the most common tuning in practice from about the 4th century BC to the 2nd century AD appears to have been Archytas's diatonic, or Ptolemy's "tonic diatonic", which has the superparticular 28/27 instead of the complex 256/243 for the lowest interval:
hypate parhypate lichanos mese | 28/27 | 8/7 | 9/8 | -498 -435 -204 0 cents
Ptolemy described his "equable" or "even diatonic" as sounding foreign or rustic, and its neutral seconds are reminiscent of scales used in Arab music. It is based on an equal division of string lengths, which implies a harmonic series of pitch frequencies:
hypate parhypate lichanos mese | 12/11 | 11/10 | 10/9 | -498 -347 -182 0 cents
Byzantine music
In Byzantine music most of the modes of the octoechos are based on the diatonic genus, apart from the second mode (both authentic and plagal) which is based on the chromatic genus. Byzantine music theory distinguishes between two tunings of the diatonic genus, the so-called "hard diatonic" on which the third mode and two of the grave modes are based, and the "soft diatonic" on which the first mode (both authentic and plagal) and the fourth mode (both authentic and plagal) are based. The hard tuning of the diatonic genus in Byzantine music may also be referred to as the enharmonic genus; an unfortunate name that persisted, since it can be confused with the ancient enharmonic genus.
Chromatic
Aristoxenus describes the chromatic genus (Greek: χρωματικό γένος or χρωματική) as a more recent development than the diatonic (Mathiesen 1999, 310). It is characterized by an upper interval of a minor third. The pyknon (πυκνόν), consisting of the two movable members of the tetrachord, is divided into two adjacent semitones.
The scale generated by the chromatic genus is not like the modern chromatic scale. The modern (18th-century) well-tempered chromatic scale has twelve pitches to the octave, and consists of semitones of various sizes; the equal temperament common today, on the other hand, also has twelve pitches to the octave, but the semitones are all of the same size. In contrast, the ancient Greek chromatic scale had seven tones to the octave (assuming alternating conjunct and disjunct tetrachords), and had incomposite minor thirds as well as semitones and whole tones.
The (Dorian) scale generated from the chromatic genus is composed of two chromatic tetrachords:

whereas in modern music theory, a chromatic scale is:
- E F F♯ G G♯ A A♯ B C C♯ D D♯ E ...
Shades
The number and nature of the shades of the chromatic genus vary amongst the Greek theorists. The major division is between the Aristoxenians and the Pythagoreans. Aristoxenus and Cleonides agree there are three, called soft, hemiolic, and tonic. Ptolemy, representing a Pythagorean view, held that there are five (Solomon 1980, 259).
Tunings
Theon of Smyrna gives an incomplete account of Thrasyllus of Mendes' formulation of the greater perfect system, from which the diatonic and enharmonic genera can be deduced. For the chromatic genus, however, all that is given is a 32:27 proportion of mese to lichanos. This leaves 9:8 for the pyknon, but there is no information at all about the position of the chromatic parhypate and therefore of the division of the pyknon into two semitones, though it may have been the limma of 256:243, as Boethius does later (Barbera 1977, 306, 309). Someone has referred to this speculative reconstructions as the traditional Pythagorean tuning of the chromatic genus:
hypate parhypate lichanos mese 4/3 81/64 32/27 1/1 | 256/243 | 2187/2048 | 32/27 | -498 -408 -294 0 centsPlay
Archytas used the simpler and more consonant 9/7, which he used in all three of his genera. His chromatic division is (Barbera 2001):
hypate parhypate lichanos mese 4/3 9/7 32/27 1/1 | 28/27 | 243/224 | 32/27 | -498 -435 -294 0 cents
According to Ptolemy's calculations, Didymus's chromatic has only 5-limit intervals, with the smallest possible numerators and denominators (Richter 2001). The successive intervals are all superparticular numbers:
hypate parhypate lichanos mese 4/3 5/4 6/5 1/1 | 16/15 | 25/24 | 6/5 | -498 -386 -316 0 cents
Byzantine music
In Byzantine music the chromatic genus is the genus on which the second mode and second plagal mode are based. The "extra" mode nenano is also based on this genus.
Enharmonic
Aristoxenus describes the enharmonic genus (Ancient Greek: [γένος] ἐναρμόνιον; Latin: enarmonium, [genus] enarmonicum, harmonia) as the "highest and most difficult for the senses" (Mathiesen 1999, 310). Historically it has been the most mysterious and controversial of the three genera. Its characteristic interval is a ditone (or major third in modern terminology), leaving the pyknon to be divided by two intervals smaller than a semitone called dieses (approximately quarter tones, though they could be calculated in a variety of ways). Because it is not easily represented by Pythagorean tuning or meantone temperament, there was much fascination with it in the Renaissance. It has nothing to do with modern uses of the term enharmonic.
Notation
Modern notation for enharmonic notes requires two special symbols for raised and lowered quarter tones or half-semitones or quarter steps. Some symbols used for a quarter-tone flat are a downward-pointing arrow ↓, or a flat combined with an upward-pointing arrow ↑. Similarly, for a quarter-tone sharp, an upward-pointing arrow may be used, or else a sharp with a downward-pointing arrow. Three-quarter flat and sharp symbols are formed similarly (Read 1964, 143). A further modern notation involves reversed flat signs for quarter-flat, so that an enharmonic tetrachord may be represented:
- D E
 F
F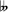 G ,
G ,
or
- A B
 C
C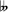 D .
D .
The double-flat symbol (![]() ) is used for modern notation of the third tone in the tetrachord to keep scale notes in letter sequence, and to remind the reader that the third tone in an enharmonic tetrachord (say F
) is used for modern notation of the third tone in the tetrachord to keep scale notes in letter sequence, and to remind the reader that the third tone in an enharmonic tetrachord (say F![]() , shown above) was not tuned quite the same as the second note in a diatonic or chromatic scale (the E♭ expected instead of F
, shown above) was not tuned quite the same as the second note in a diatonic or chromatic scale (the E♭ expected instead of F![]() ).
).
Scale
Like the diatonic scale, the ancient Greek enharmonic scale also had seven notes to the octave (assuming alternating conjunct and disjunct tetrachords), not 24 as one might imagine by analogy to the modern chromatic scale (West 1992, 254–73). A scale generated from two disjunct enharmonic tetrachords is:
- D E
 F
F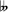 G - A B
G - A B C
C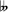 D or, in music notation starting on E:
D or, in music notation starting on E: 
 Play ,
Play ,
with the corresponding conjunct tetrachords forming
- A B
 C
C D E
D E F
F G or, transposed to E like the previous example:
G or, transposed to E like the previous example: 
 Play .
Play .
Tunings
The precise ancient Pythagorean tuning of the enharmonic genus is not known (Chalmers 1990, 9). Aristoxenus believed that the pyknon evolved from an originally pentatonic trichord in which a perfect fourth was divided by a single "infix"—an additional note dividing the fourth into a semitone plus a major third (e.g., E, F, A, where F is the infix dividing the fourth E–A). Such a division of a fourth necessarily produces a scale of the type called pentatonic, because compounding two such segments into an octave produces a scale with just five steps. This became an enharmonic tetrachord by the division of the semitone into two quarter tones (E, E↑, F, A) (West 1992, 163).
Archytas, according to Ptolemy, Harmonics, ii.14—for no original writings by him survive (Mathiesen 2001b, (i) Pythagoreans)—as usual gives a tuning with small-number ratios (Chalmers 1990, 9):
hypate parhypate lichanos mese 4/3 9/7 5/4 1/1 | 28/27 |36/35| 5/4 | -498 -435 -386 0 centsPlay
Also according to Ptolemy, Didymus uses the same major third (5/4) but divides the pyknon with the arithmetic mean of the string lengths (if one wishes to think in terms of frequencies, rather than string lengths or interval distance down from the tonic, as the example below does, splitting the interval between the frequencies 3/4 and 4/5 by their harmonic mean 24/31 will result in the same sequence of intervals as below) (Chalmers 1990, 9):
hypate parhypate lichanos mese 4/3 31/24 5/4 1/1 |32/31 |31/30 | 5/4 | -498 -443 -386 0 cents
This method splits the 16/15 half-step pyknon into two nearly equal intervals, the difference in size between 31/30 and 32/31 being less than 2 cents.
Rhythms
The principal theorist of rhythmic genera was Aristides Quintilianus, who considered there to be three: equal (dactylic or anapestic), sesquialteran (paeonic), and duple (iambic and trochaic), though he also admitted that some authorities added a fourth genus, sesquitertian (Mathiesen 2001a).
Sources
- Barbera, C. André. 1977. "Arithmetic and Geometric Divisions of the Tetrachord". Journal of Music Theory 21, no. 2 (Autumn): 294–323.
- Barbera, André. 2001. "Archytas of Tarentum". The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell. London: Macmillan Publishers.
- Chalmers, John. 1990. Divisions of the Tetrachord. Lebanon NH: Frog Peak Music. ISBN 0-945996-04-7.
- Drabkin, William. 1980. "Diatonic". The New Grove Dictionary of Music and Musicians, first edition, edited by Stanley Sadie. London: Macmillan Publishers.
- Dunsby, Jonathan. 2002. "Diatonic". The Oxford Companion to Music, edited by Alison Latham. Oxford and New York.
- Mathiesen, Thomas J. 1999 Apollo's Lyre: Greek Music and Music Theory in Antiquity and the Middle Ages. Publications of the Center for the History of Music Theory and Literature 2. Lincoln and London: University of Nebraska Press. ISBN 9780803230798.
- Mathiesen, Thomas J. 2001a. "Genus". The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell. London: Macmillan Publishers.
- Mathiesen, Thomas J. 2001b"Greece, §I: Ancient, 6: Music Theory (iii): Aristoxenian Tradition, (c) Genera". The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell. London: Macmillan Publishers.
- Read Gardner, Music Notation: A Manual of Modern Practice. Boston: Allyn and Bacon, Inc.
- Richter, Lukas. 2001. "Didymus [Didymos ho mousikos]". The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell. London: Macmillan Publishers.
- Solomon, Jon. 1980. "Cleonides: Εἰσαγωγὴ ἁρμονική [Eisagogē harmonikē]; Critical Edition, Translation, and Commentary". PhD diss. Chapel Hill: University of North Carolina, Chapel Hill.
- West, Martin Litchfield. 1992. Ancient Greek Music. Oxford: Clarendon Press. ISBN 0-19-814975-1.