Dawson function
In mathematics, the Dawson function or Dawson integral (named after H. G. Dawson[1]) is either
- ,
also denoted as F(x) or D(x), or alternatively
- .
The Dawson function is the one-sided Fourier-Laplace sine transform of the Gaussian function,
It is closely related to the error function erf, as
where erfi is the imaginary error function, erfi(x) = −i erf(ix). Similarly,
in terms of the real error function, erf.
In terms of either erfi or the Faddeeva function w(z), the Dawson function can be extended to the entire complex plane:[2]
- ,
which simplifies to
for real x.
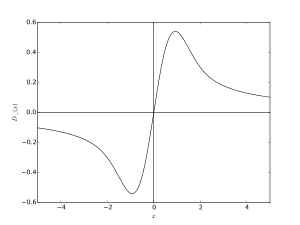
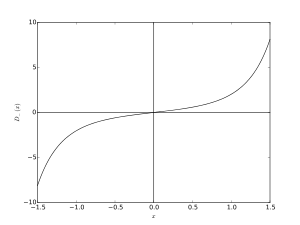
For |x| near zero, F(x) ≈ x, and for |x| large, F(x) ≈ 1/(2x). More specifically, near the origin it has the series expansion
- ,
while for large x it has the asymptotic expansion
- ,
where n!! is the double factorial.
F(x) satisfies the differential equation
with the initial condition F(0) = 0. Consequently, it has extrema for
- ,
resulting in x = ±0.92413887… (![]() A133841), F(x) = ±0.54104422… (
A133841), F(x) = ±0.54104422… (![]() A133842).
A133842).
Inflection points follow for
- ,
resulting in x = ±1.50197526… (![]() A133843), F(x) = ±0.42768661… (
A133843), F(x) = ±0.42768661… (![]() A245262). (Apart from the trivial inflection point at x = 0, F(x) = 0.)
A245262). (Apart from the trivial inflection point at x = 0, F(x) = 0.)
Relation to Hilbert transform of Gaussian
The Hilbert Transform of the Gaussian is defined as
P.V. denotes the Cauchy principal value, and we restrict ourselves to real . can be related to the Dawson function as follows. Inside a principal value integral, we can treat as a generalized function or distribution, and use the Fourier representation
With , we use the exponential representation of and complete the square with respect to to find
We can shift the integral over to the real axis, and it gives . Thus
We complete the square with respect to and obtain
We change variables to :
The integral can be performed as a contour integral around a rectangle in the complex plane. Taking the imaginary part of the result gives
where is the Dawson function as defined above.
The Hilbert transform of is also related to the Dawson function. We see this with the technique of differentiating inside the integral sign. Let
Introduce
The nth derivative is
We thus find
The derivatives are performed first, then the result evaluated at . A change of variable also gives . Since , we can write where and are polynomials. For example, . Alternatively, can be calculated using the recurrence relation (for )
- .
References
- Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 6.9. Dawson's Integral", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Temme, N. M. (2010), "Error Functions, Dawson's and Fresnel Integrals", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248
- ↑ Dawson, H. G. (1897). "On the Numerical Value of ". Proceedings of the London Mathematical Society. s1-29 (1): 519–522. doi:10.1112/plms/s1-29.1.519.
- ↑ Mofreh R. Zaghloul and Ahmed N. Ali, "Algorithm 916: Computing the Faddeyeva and Voigt Functions," ACM Trans. Math. Soft. 38 (2), 15 (2011). Preprint available at arXiv:1106.0151.
External links
- gsl_sf_dawson in the GNU Scientific Library
- Cephes – C and C++ language special functions math library
- Faddeeva Package – C++ code for the Dawson function of both real and complex arguments, via the Faddeeva function
- Dawson's Integral (at Mathworld)
- Error functions