Cut-insertion theorem
The Cut-insertion theorem, also known as Pellegrini's theorem,[1] is a linear network theorem that allows transformation of a generic network N into another network N' that makes analysis simpler and for which the main properties are more apparent.
Statement

Let e, h, u, w, q=q', and t=t' be six arbitrary nodes of the network N and 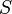 be an independent voltage or current source connected between e and h, while
be an independent voltage or current source connected between e and h, while 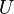 is the output quantity, either a voltage or current, relative to the branch with immittance
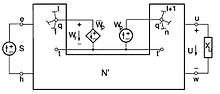
is the output quantity, either a voltage or current, relative to the branch with immittance 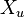 , connected between u and w. Let us now cut the qq' connection and insert a three-terminal circuit ("TTC") between the two nodes q and q' and the node t=t' , as in figure b (
, connected between u and w. Let us now cut the qq' connection and insert a three-terminal circuit ("TTC") between the two nodes q and q' and the node t=t' , as in figure b (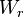 and
and 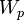 are homogeneous quantities, voltages or currents, relative to the ports qt and q'q't' of the TTC).
are homogeneous quantities, voltages or currents, relative to the ports qt and q'q't' of the TTC).
In order for the two networks N and N' to be equivalent for any 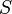 , the two constraints
, the two constraints 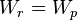 and
and 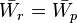 , where the overline indicates the dual quantity, are to be satisfied.
, where the overline indicates the dual quantity, are to be satisfied.
The above mentioned three-terminal circuit can be implemented, for example, connecting an ideal independent voltage or current source 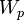 between q' and t' , and an immittance
between q' and t' , and an immittance 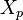 between q and t.
between q and t.
Network functions
With reference to the network N', the following network functions can be defined:
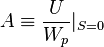 ;
; 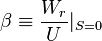 ;
; 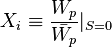
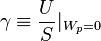 ;
; 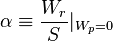 ;
; 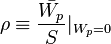
from which, exploiting the Superposition theorem, we obtain:
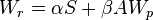
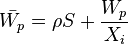 .
.
Therefore the first constraint for the equivalence of the networks is satisfied if 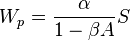 .
.
Furthermore,
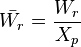
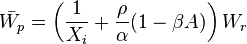
therefore the second constraint for the equivalence of the networks holds if 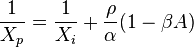 [2]
[2]
Transfer function
If we consider the expressions for the network functions 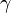 and
and 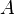 , the first constraint for the equivalence of the networks, and we also consider that, as a result of the superposition principle,
, the first constraint for the equivalence of the networks, and we also consider that, as a result of the superposition principle, 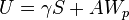 , the transfer function
, the transfer function 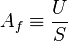 is given by
is given by
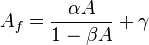 .
.
For the particular case of a feedback amplifier, the network functions 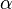 ,
, 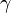 and
and 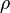 take into account the nonidealities of such amplifier. In particular:
take into account the nonidealities of such amplifier. In particular:
-
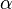 takes into account the nonideality of the comparison network at the input
takes into account the nonideality of the comparison network at the input -
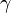 takes into account the non unidirectionality of the feedback chain
takes into account the non unidirectionality of the feedback chain -
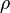 takes into account the non unidirectionality of the amplification chain.
takes into account the non unidirectionality of the amplification chain.
If the amplifier can be considered ideal, i.e. if 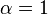 ,
, 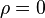 and
and 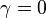 , the transfer function reduces to the known expression deriving from classical feedback theory:
, the transfer function reduces to the known expression deriving from classical feedback theory:
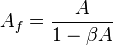 .
.
Evaluation of the impedance and of the admittance between two nodes
The evaluation of the impedance (or of the admittance) between two nodes is made somewhat simpler by the cut-insertion theorem.
Impedance

Let us insert a generic source 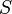 between the nodes j=e=q and k=h between which we want to evaluate the impedance
between the nodes j=e=q and k=h between which we want to evaluate the impedance 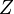 . By performing a cut as shown in the figure, we notice that the immittance
. By performing a cut as shown in the figure, we notice that the immittance 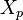 is in series with
is in series with 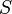 and the current through it is thus the same as that provided by
and the current through it is thus the same as that provided by 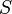 . If we choose an input voltage source
. If we choose an input voltage source 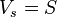 and, as a consequence, a current
and, as a consequence, a current 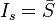 , and an impedance
, and an impedance 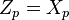 , we can write the following relationships:
, we can write the following relationships:
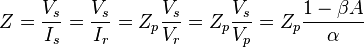 .
.
Considering that 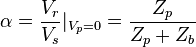 , where
, where 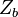 is the impedance seen between the nodes k=h and t if remove
is the impedance seen between the nodes k=h and t if remove 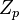 and short-circuit the voltage sources, we obtain the impedance
and short-circuit the voltage sources, we obtain the impedance 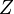 between the nodes j and k in the form:
between the nodes j and k in the form:
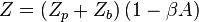
Admittance
We proceed in a way analogous to the impedance case, but this time the cut will be as shown in the figure to the right, noticing that 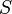 is now in parallel to
is now in parallel to 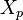 . If we consider an input current source
. If we consider an input current source 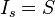 (as a result we have a voltage
(as a result we have a voltage 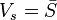 ) and an admittance
) and an admittance 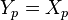 , the admittance
, the admittance 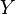 between the nodes j and k can be computed as follows:
between the nodes j and k can be computed as follows:
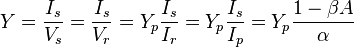 .
.
Considering that 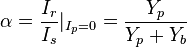 , where
, where 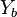 is the admittance seen between the nodes k=h and t if we remove
is the admittance seen between the nodes k=h and t if we remove 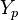 and open the current sources, we obtain the admittance
and open the current sources, we obtain the admittance 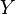 in the form:
in the form:
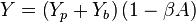
Comments
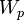 and a dependent source
and a dependent source 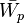 .
.The implementation of the TTC with an independent source 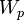 and an immittance
and an immittance 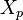 is useful and intuitive for the calculation of the impedance between two nodes, but involves, as in the case of the other network functions, the difficulty of the calculation of
is useful and intuitive for the calculation of the impedance between two nodes, but involves, as in the case of the other network functions, the difficulty of the calculation of 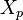 from the equivalence equation. Such difficulty can be avoided using a dependent source
from the equivalence equation. Such difficulty can be avoided using a dependent source 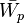 in place of
in place of 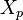 and using the Blackman formula[3] for the evaluation of
and using the Blackman formula[3] for the evaluation of 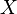 . Such an implementation of the TTC allows finding a feedback topology even in a network consisting of a voltage source and two impedances in series.
. Such an implementation of the TTC allows finding a feedback topology even in a network consisting of a voltage source and two impedances in series.
Notes
- ↑ Bruno Pellegrini has been the first Electronic Engineering graduate at the University of Pisa where is currently Professor Emeritus. He is also author of the Electrokinematics theorem, that connects the velocity and the charge of carriers moving inside an arbitrary volume to the currents, voltages and power on its surface through an arbitrary irrotational vector.
- ↑ Notice that for the evaluation of Xp we need network functions that depend, in their turn, on Xp. To proceed with calculations, it is therefore appropriate to perform a cut for which ρ=0, so that Xp=Xi.
- ↑ R. B. Blackman, Effect of Feedback on Impedance, Bell System Tech. J. 22, 269 (1943).
References
- B. Pellegrini, Considerations on the Feedback Theory, Alta Frequenza 41, 825 (1972).
- B. Pellegrini, Improved Feedback Theory, IEEE Transactions on Circuits and Systems 56, 1949 (2009).