Conchoid of Dürer

Conchoid of Dürer, constructed by him

The conchoid of Dürer, also called Dürer's shell curve, is a variant of a conchoid or plane algebraic curve, named after Albrecht Dürer. It is not a true conchoid.

Construction

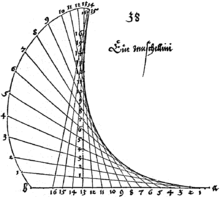
Let Q and R be points moving on a pair of perpendicular lines which intersect at O in such a way that OQ + OR is constant. On any line QR mark point P at a fixed distance from Q. The locus of the points P is Dürer's conchoid.

Equation

The equation of the conchoid in Cartesian form is

2y^{2}(x^{2}+y^{2})-2by^{2}(x+y)+(b^{2}-3a^{2})y^{2}-a^{2}x^{2}+2a^{2}b(x+y)+a^{2}(a^{2}-b^{2})=0.\,

Properties

The curve has two components, asymptotic to the lines $y=\pm a/{\sqrt {2}}$ . Each component is a rational curve. If a>b there is a loop, if a=b there is a cusp at (0,a).

Special cases include:

a=0: the line y=0;
b=0: the line pair $y=\pm x/{\sqrt {2}}$ together with the circle $x^{2}+y^{2}=a^{2}$ ;

History

It was first described by the German painter and mathematician Albrecht Dürer (1471–1528) in his book Underweysung der Messung (S. 38), calling it Ein muschellini.

References

J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 157–159. ISBN 0-486-60288-5.

This article is issued from Wikipedia - version of the 8/20/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.