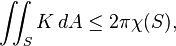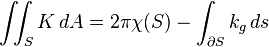Cohn-Vossen's inequality

In differential geometry, Cohn-Vossen's inequality, named after Stephan Cohn-Vossen, relates the integral of Gaussian curvature of a non-compact surface to the Euler characteristic. It is akin to the Gauss–Bonnet theorem for a compact surface.

A divergent path within a Riemannian manifold is a smooth curve in the manifold that is not contained within any compact subset of the manifold. A complete manifold is one in which every divergent path has infinite length with respect to the Riemannian metric on the manifold. Cohn-Vossen's inequality states that in every complete Riemannian 2-manifold S with finite total curvature and finite Euler characteristic, we have^[1]

where K is the Gaussian curvature, dA is the element of area, and χ is the Euler characteristic.

Examples

• If S is a compact surface (without boundary), then the inequality is an equality by the usual Gauss–Bonnet theorem for compact manifolds.
• If S has a boundary, then the Gauss–Bonnet theorem gives

where 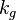is the geodesic curvature of the boundary, and its integral the total curvature which is necessarily positive for a boundary curve, and the inequality is strict. (A similar result holds when the boundary of S is piecewise smooth.)

• If S is the plane R², then the curvature of S is zero, and χ(S) = 1, so the inequality is strict: 0 < 2π.

Notes and references

• S. E. Cohn-Vossen, Some problems of differential geometry in the large, Moscow (1959) (in Russian)

External links

• Gauss–Bonnet theorem, in the Encyclopedia of Mathematics, including a brief account of Cohn-Vossen's inequality