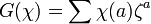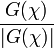Chowla–Mordell theorem

In mathematics, the Chowla–Mordell theorem is a result in number theory determining cases where a Gauss sum is the square root of a prime number, multiplied by a root of unity. It was proved and published independently by Sarvadaman Chowla and Louis Mordell, around 1951.

In detail, if 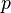$p$ is a prime number, 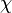$\chi$ a nontrivial Dirichlet character modulo 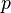$p$ , and

G(\chi)=\sum \chi(a) \zeta^a

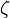where $\zeta$ is a primitive 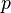$p$ -th root of unity in the complex numbers, then

\frac{G(\chi)}{|G(\chi)|}

is a root of unity if and only if 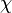$\chi$ is the quadratic residue symbol modulo 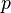$p$ . The 'if' part was known to Gauss: the contribution of Chowla and Mordell was the 'only if' direction. The ratio in the theorem occurs in the functional equation of L-functions.

References

Gauss and Jacobi Sums by Bruce C. Berndt, Ronald J. Evans and Kenneth S. Williams, Wiley-Interscience, p. 53.

This article is issued from Wikipedia - version of the 4/20/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.