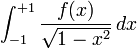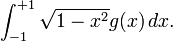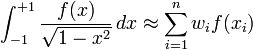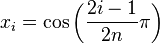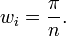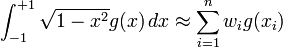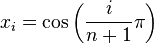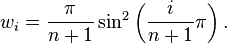Chebyshev–Gauss quadrature

In numerical analysis Chebyshev–Gauss quadrature is an extension of Gaussian quadrature method for approximating the value of integrals of the following kind:

\int_{-1}^{+1} \frac {f(x)} {\sqrt{1 - x^2} }\,dx

and

\int_{-1}^{+1} \sqrt{1 - x^2} g(x)\,dx.

In the first case

\int_{-1}^{+1} \frac {f(x)} {\sqrt{1-x^2} }\,dx \approx \sum_{i=1}^n w_i f(x_i)

where

x_i = \cos \left( \frac {2i-1} {2n} \pi \right)

and the weight

w_i = \frac {\pi} {n}.[1]

In the second case

\int_{-1}^{+1} \sqrt{1-x^2} g(x)\,dx \approx \sum_{i=1}^n w_i g(x_i)

where

x_i = \cos \left( \frac {i} {n+1} \pi \right)

and the weight

w_i = \frac {\pi} {n+1} \sin^2 \left( \frac {i} {n+1} \pi \right). \,[2]

See also

References

  1. ↑ Abramowitz, M & Stegun, I A, Handbook of Mathematical Functions, 10th printing with corrections (1972), Dover, ISBN 978-0-486-61272-0. Equation 25.4.38.
  2. ↑ Abramowitz, M & Stegun, I A, Handbook of Mathematical Functions, 10th printing with corrections (1972), Dover, ISBN 978-0-486-61272-0. Equation 25.4.40.

External links

This article is issued from Wikipedia - version of the 4/20/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.