Apeirogon

See also: Skew apeirogon
Regular apeirogon
Edges and vertices ∞
Schläfli symbol {∞}
Coxeter diagram
Dual polygon Self-dual
The interior of a linear apeirogon can be defined by a counterclockwise orientation of vertices, as shown by arrows on the edges here, defining the top half plane in this picture.
Two such apeirogons can therefore fill the plane, as a regular tiling and vertex configuration ∞.∞.

In geometry, an apeirogon is a generalized polygon with a countably infinite number of sides.[1] It can be considered as the limit of an n-sided polygon as n approaches infinity. The interior of a linear apeirogon can be defined by a direction order of vertices, and defining half the plane as the interior.

This article describes an apeirogon in its linear form as a tessellation or partition of a line.

Regular apeirogon

A regular apeirogon has equal edge lengths, just like any regular polygon, {p}. Its Schläfli symbol is {∞}, and its Coxeter-Dynkin diagram is . It is the first in the dimensional family of regular hypercubic honeycombs.

This line may be considered as a circle of infinite radius, by analogy with regular polygons with great number of edges, which resemble a circle.

In two dimensions, a regular apeirogon divides the plane into two half-planes as a regular apeirogonal dihedron. The interior of an apeirogon can be defined by its orientation, filling one half plane. Dually the apeirogonal hosohedron has digon faces and an apeirogonal vertex figure, {2, ∞}. A truncated apeirogonal hosohedron becomes a apeirogonal prism, with each vertex bounded by two squares and an apeirogon. An alternated apeirogonal prism is a apeirogonal antiprism, with each vertex bounded by three triangles and an apeirogon.

Euclidean tilings
Regular Uniform
∞.∞ 2∞ 4.4.∞ 3.3.3.∞
{∞, 2}
 {2, ∞}
 t{2, ∞}
 sr{2, ∞}

The regular apeirogon can also be seen as linear sets within 4 of the regular, uniform tilings, and 5 of the uniform dual tilings in the Euclidean plane.

3 directions 1 direction 2 directions

Hexadeltille
Deltile
Isosnub quadrille
Quadrille
3 directions 6 directions 1 direction 4 directions

Tetrille
Kisdeltile
Kisrhombille
iso(4-)pentille
Kisquadrille

Irregular apeirogon

An isogonal apeirogon has a single type of vertex and alternates two types of edges.

A quasiregular apeirogon is an isogonal apeirogon with equal edge lengths.

An isotoxal apeirogon, being the dual of an isogonal one, has one type of edge, and two types of vertices, and is therefore geometrically identical to the regular apeirogon. It can be shown seen by drawing vertices in alternate colors.

All of these will have half the symmetry (double the fundamental domain sizes) of the regular apeirogon.

Regular ... ...
Quasiregular ... ...
Isogonal ... ...
Isotoxal ... ...

Apeirogons in hyperbolic plane

an apeirogon and circumscribed horocycle

Apeirogons in the hyperbolic plane, most notably the regular apeirogon, {∞}, can have a curvature just like finite polygons of the Euclidean plane, with the vertices circumscribed by horocycles or hypercycles rather than circles.

Regular apeirogons that are scaled to converge at infinity have the symbol {∞} and exist on horocycles, while more generally they can exist on hypercycles.

The regular tiling {∞, 3} has regular apeirogon faces. Hypercyclic apeirogons can also be isogonal or quasiregular, with truncated apeirogon faces, t{∞}, like the tiling tr{∞,3}, with two types of edges, alternately connecting to triangles or other apeirogons.

uniform tilings with apeirogons
3 4 5

{∞,3}
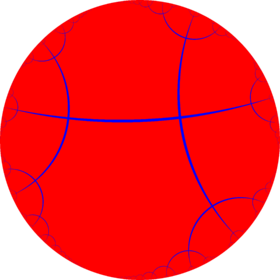{∞,4}
{∞,5}
uniform tilings with apeirogons (cont.)
6 7 8 ... ∞

{∞,6}
{∞,7}
{∞,8}
{∞,∞}
Regular and uniform tilings with apeirogons
{∞, 3} tr{∞, 3} tr{12i, 3}

Regular: {∞}
Quasiregular: t{∞}
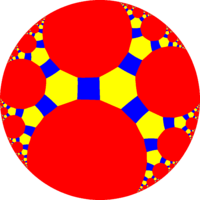Quasiregular: t{12i}

Pseudogon

A regular pseudogon, {iπ/λ}, the Poincaré disk model, with perpendicular reflection lines shown, separated by length λ.

Norman Johnson calls the general apeirogon (divergent mirror form) a pseudogon, circumscribed by a hypercycle, with and regular pseudogons as {iπ/λ}, where λ is the periodic distance between the divergent perpendicular mirrors.[2]

See also

References

  1. ↑ Coxeter, Regular polytopes, p.45
  2. ↑ Norman Johnson, Geometries and symmetries, (2015), Chapter 11. Finite symmetry groups, Section 11.2 The polygonal groups. p.141

External links

This article is issued from Wikipedia - version of the 10/18/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.